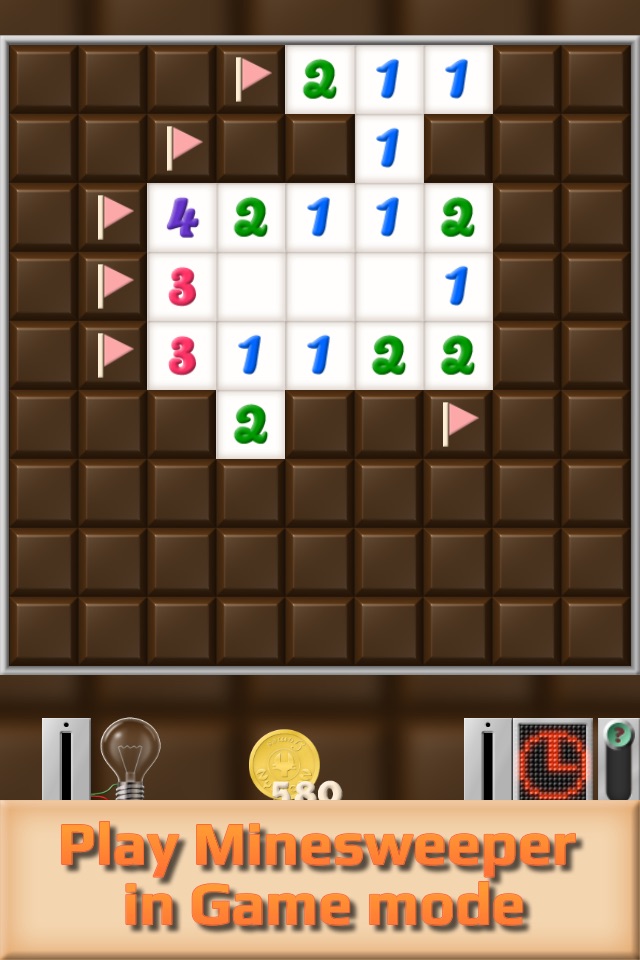
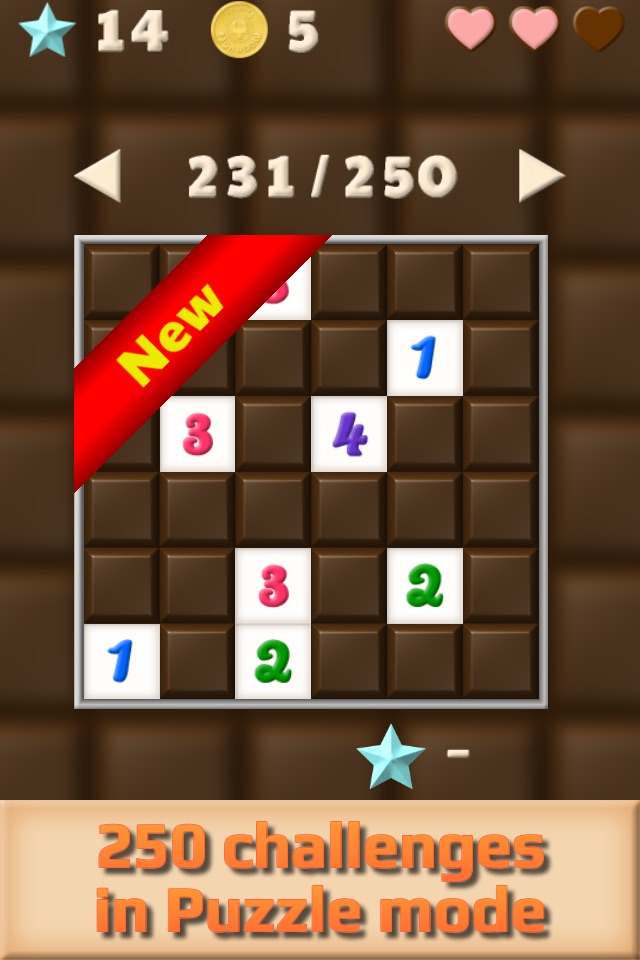
Nyahoon Games proudly presents the most difficult Minesweeper ever!
How difficult can it be? Richard Kaye proved that Minesweeper is NP-complete[1,2]. That means Minesweeper can be a very difficult problem even for computers to solve.
We made up such Minesweeper into a "perfect" puzzle game. I use "perfect" to mean that no guesses are required to solve puzzles, or even more strictly, no guesses are allowed. Only the squares (means "chocolate cubes" in this game) that are certainly safe can be uncovered (eaten).
This game has two play modes, Game and Puzzle. Puzzle mode has 250 challenging puzzles. In Game mode, you can play random puzzles like standard Minesweeper, but they are guess-free. You will never get tired of playing!
Once you play this game, you will realize that Minesweeper was such a difficult, but very fun puzzle game.
Some other puzzle games, such as Number Place (aka Sudoku) and Nonogram (aka Hanjie, Picross or Griddlers), are also proven as NP-complete[3,4,5]. Therefore, I can say this game is as much fun as those puzzle games.
Chocolate Sweeper is optimized for mobile screen size and touch interface. This is the best puzzle game you can play on a mobile device!
Please be cautioned that this game is not as sweet as it looks. It is really difficult, and not recommended for those people who just want to play games for relaxation.
This App will collect some user information for ads and analytics. Please understand and agree with our privacy policy (updated on 25 April 2016).
References
[1] Richard Kayes Minesweeper Pages: http://web.mat.bham.ac.uk/R.W.Kaye/minesw/minesw.htm
[2] R. Kaye. Minesweeper is NP-complete. Mathematical Intelligencer, 22(2):9–15, 2000.
[3] T. Yato. List of NP-Complete Pencil Puzzles: http://www-imai.is.s.u-tokyo.ac.jp/~yato/data2/puzcc.pdf
[4] T. Yato and T. Seta. Complexity and completeness of finding another solution and its application to puzzles. IPSJ SIG Notes 2002-AL-87-2, IPSJ, 2002. http://www-imai.is.s.u-tokyo.ac.jp/~yato/data2/SIGAL87-2.pdf
[5] N. Ueda and T. Nagao. NP-completeness results for NONOGRAM via parsimonious reductions. Technical Report TR96-0008, Department of Computer Science, Tokyo Institute of Technology, 1996.
=====================================================
This App uses free sound assets available from the following websites. We acknowledge their substantial contributions with many thanks.
- BGM
MusMus: http://musmus.main.jp/
- BGM/Jingle/Sound Effects
Pocket Sound: http://pocket-se.info/
- Sound Effects
Kurage-Kosho: http://www.kurage-kosho.info/
Music is VFR: http://musicisvfr.com/